Articles

Learn how to verify and standardize addresses with USPS, understand its limitations and see better options.

ZIP+4 Codes are the last 4 digits of a nine-digit ZIP Code. A nine-digit ZIP Code is made of two parts.

How to lookup county FIPS Codes by address, ZIP Code and city. County FIPS Codes are 5-digit numbers that identify each county in the United States.

With millions of addresses in the US alone, it can be a pain to ensure that your database is accurate. See how Smarty ensures accuracy for the city of Miami.

Address Line 1 contains house numbers, street names, and suffixes, among other data points. We've compiled all you need to know here, check it out now!
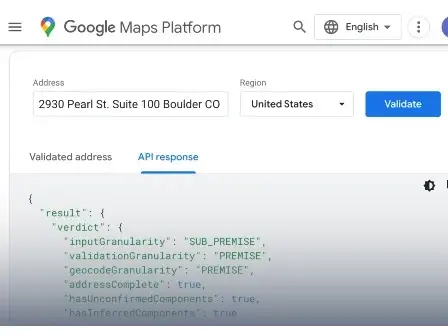
Check out how Google's address validation API stacks up against Smarty's legendary and lightning-fast address validation API. We have all you need here!
Chat with us
Real humans. Quick answers. .
General communication
For general inquiries, contact us.